Patterns from the 2-adic Valuations of N
For more on this project, click here.
It is helpful to think of the algorithm employed by the number line app as a type of Lindenmayer System or one of the other traditional fractal construction algorithms. (See, e.g., these links: Dragon Curve, Koch Snowflake, space-filling curves.)
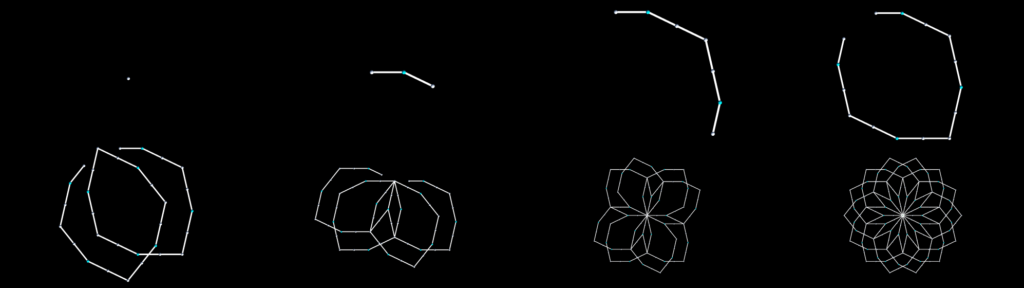
The basic idea is that you have a series of steps that you perform from beginning to end, and then you repeat those steps as many times as you wish. For example, you might have something like this:
Start with a single, straight line segment. Then:
- Find the midpoint of each line segment in the figure so far
- Create two new line segments for each line segment so far, by “folding” each of the current line segments clockwise at its midpoint to an angle of 90 degrees.
Doing steps 1 and 2 once would be “one iteration.” Repeating them a second time would be “two iterations.” And if you repeated them an infinite number of times, you’d end up with the complete Levy C-Curve.
Of course, no one has enough time to do anything an infinite number of times, so we content ourselves with “approximations” of the “true” fractals. That is, we just run through the series of steps needed to produce the fractal enough times (we go through enough “iterations”) that we can get a clear idea of what the ultimate fractal would look like.
In the number line app, the analog for iterations is the length of the number line. First, you choose which “base” number to derive patterns from. Then, you tell the app to which power of that base number it should extend the line. Doing so tells the app how many times to repeat the algorithm that produces the pattern.
For example, if you ask the app to give you the number line up to 53, it will give you a line from 1 to 124 (which is 53-1; since we start at 1, we have dropped 0, the “first” number on the line, and thus have to drop the last number as well to maintain symmetry). In the process, the app will run through the algorithm needed to produce the 5adic valuations of N three times.
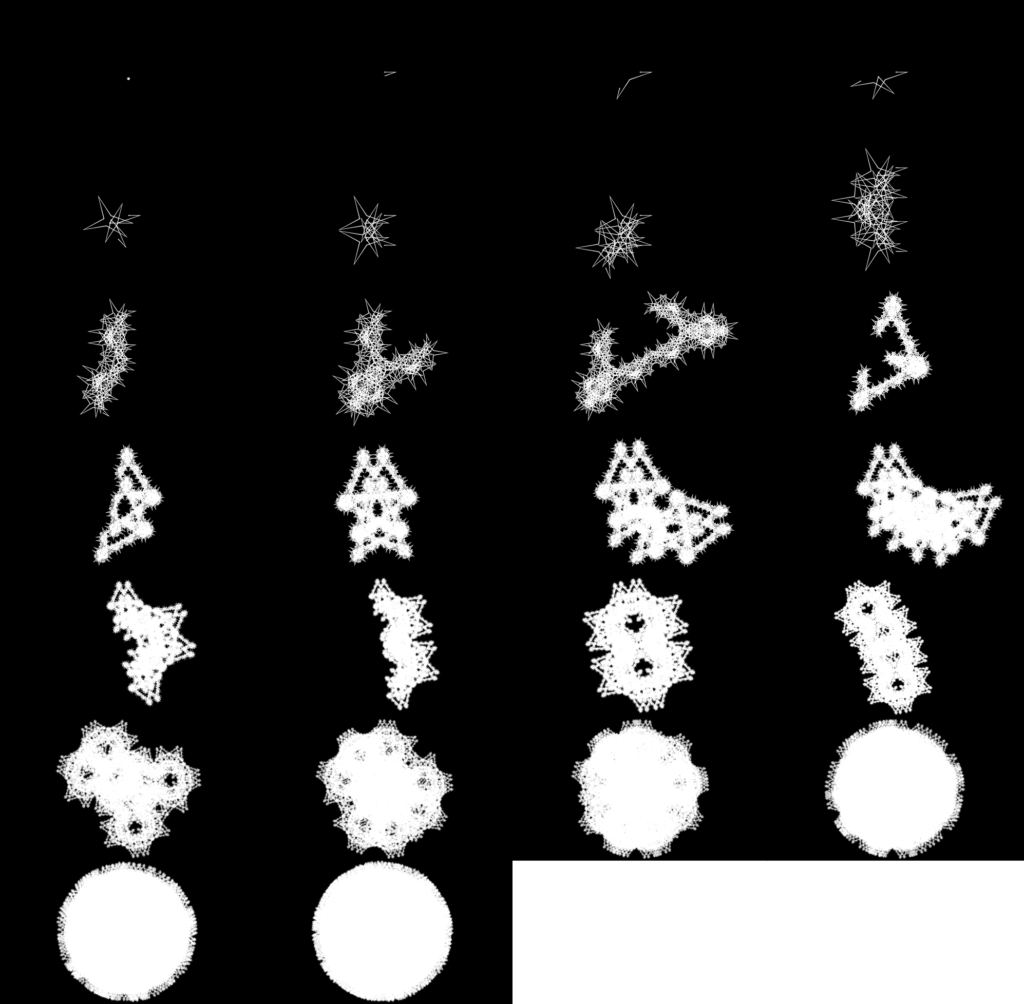
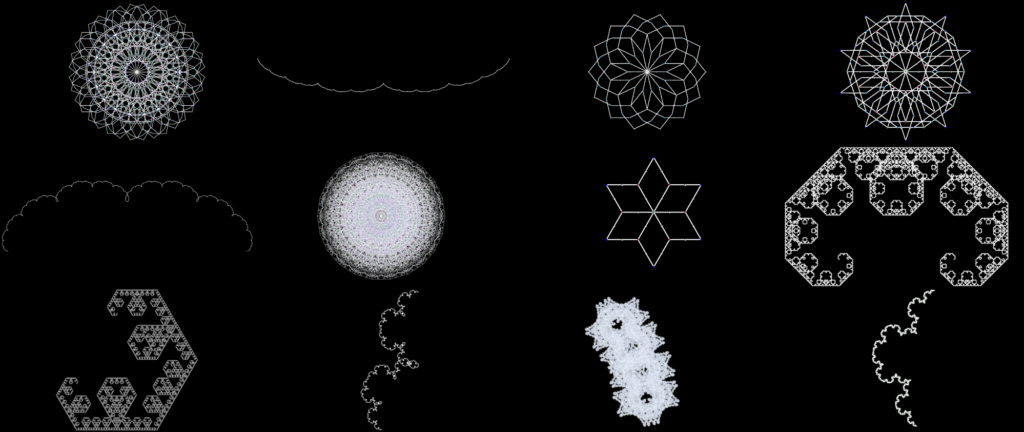
Three Types of Pattern
I have collected some of my favorite patterns created by the “2adic valuations of N” below. As you will see, they fall into three categories: fractals, fill-ins, and fuzzies. The difference between them is this:
With a fractal, as you increase the number of iterations, you get larger and larger — more and more detailed — versions of the same pattern. However, the odd thing about some of the fractals below is that they are cyclical. That is, instead of each iteration giving you a larger, more detailed form of the same pattern, you get a cycle of multiple repeating patterns from iteration to iteration. This makes it unclear which of the patterns is the “final” form of the fractal — in fact, it implies that the fractal either has no final form, or that it has multiple final forms.
In light of the fact that so many of the fractals “cycle” through multiple forms, I think it best to identify the traditional fractals — the ones that repeat the same form each iteration — as also being cyclical. It’s just that they have a cycle of length “1.” That is, instead of repeating their forms every three or seven iterations (or whatever), they repeat their forms every one iteration. (They give you the same form each time.)
With a “fill-in,” in contrast, the number line seems to be filling in (or “out,” whichever you prefer) a pattern that is not clear at first. From one iteration to the next, you are not getting larger, more detailed versions of the same pattern, nor are you getting a cycle of several repeating patterns. Instead, you have the sense that you are adding pieces to a jigsaw puzzle, and eventually there comes a point where the pattern is completely “filled in.” After that point, adding further iterations simply leads to the number line “retracing” the same path over and over.
Then, there is a third category of patterns, which I hope an insightful post-structuralist will one day use in an influential deconstruction of my work. I call them “fuzzies.”
Though all the fractals, fill-ins, and fuzzies produced by the 2adic valuations have the same underlying structure — and though that structure is fractal — adding further iterations to a fuzzy neither produces larger, more detailed versions of the same pattern (as with fractals), nor do they ever seem to “settle down” into retracing a distinct path (as with fill-ins).
Base Angle: 20 degrees (pi/9 radians)
Shape Type: Fill-In (complete from 12 iterations on)
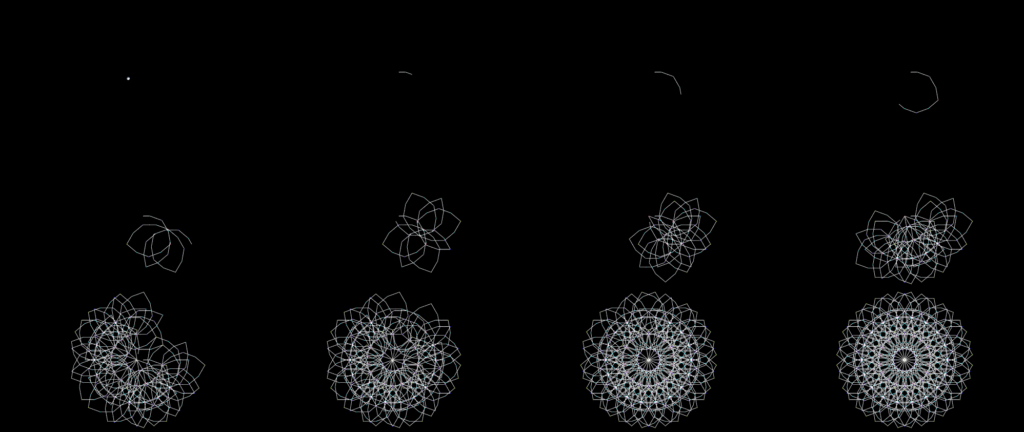
The patterns that show up in the animation seem to fall into three categories: fractals, finite patterns, and . . . everything else.
Base Angle: 22.5 degrees (pi/9 radians)
Shape Type: Fractal (1-iteration cycle)

Base Angle: 25.71 degrees (pi/7 radians)
Shape Type: Fill-In (complete from 8 iterations on)
Base Angle: 36 degrees (pi/5 radians)
Shape Type: Fill-In (complete from 9 iterations on)
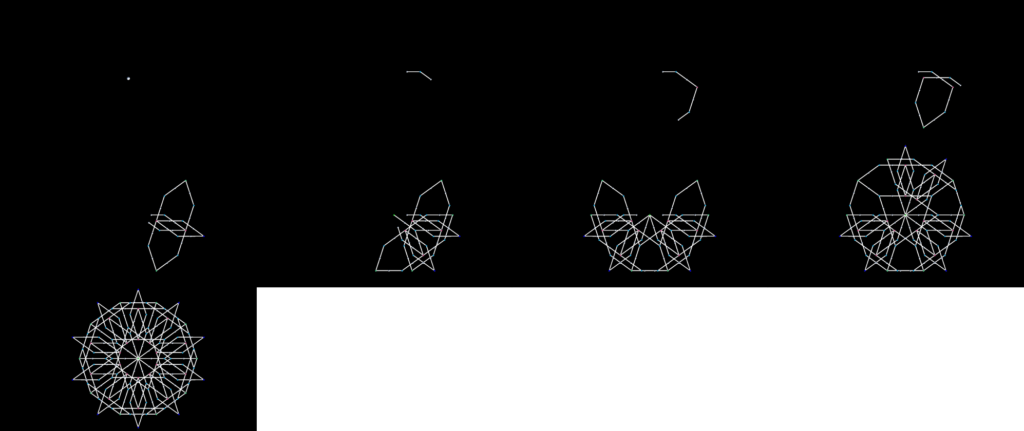
Base Angle: 42.86 degrees (5pi/21 radians)
Shape Type: Fill-In (complete from 14 iterations on)

Base Angle: 45 degrees (pi/4 radians)
Shape Type: Fractal (1-iteration cycle)

Base Angle: 48 degrees (4pi/15 radians)
Shape Type: Fractal (4-iteration cycle)
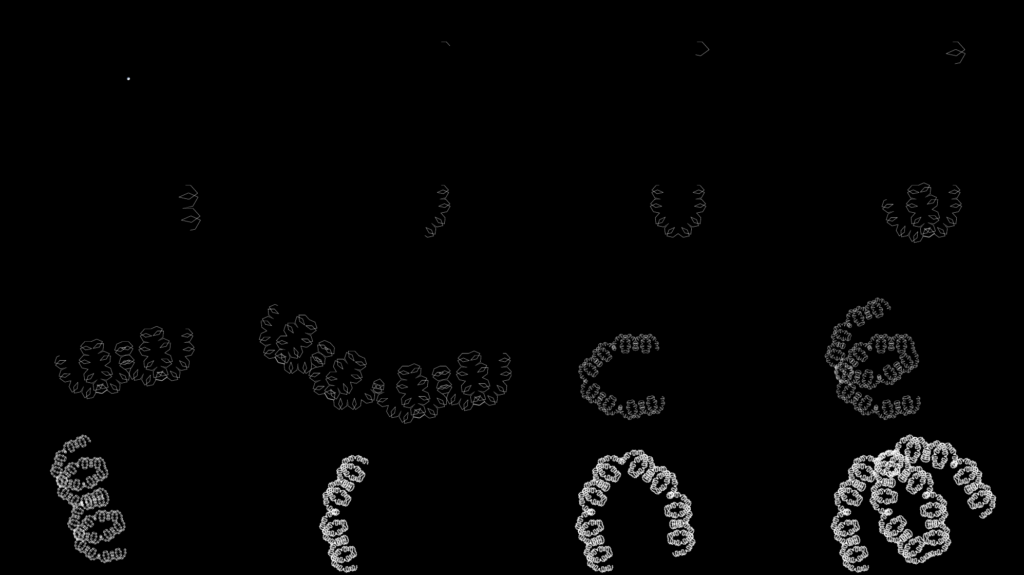
Base Angle: 49.09 degrees (3pi/11 radians)
Shape Type: Fill-In (complete from 16 iterations on)
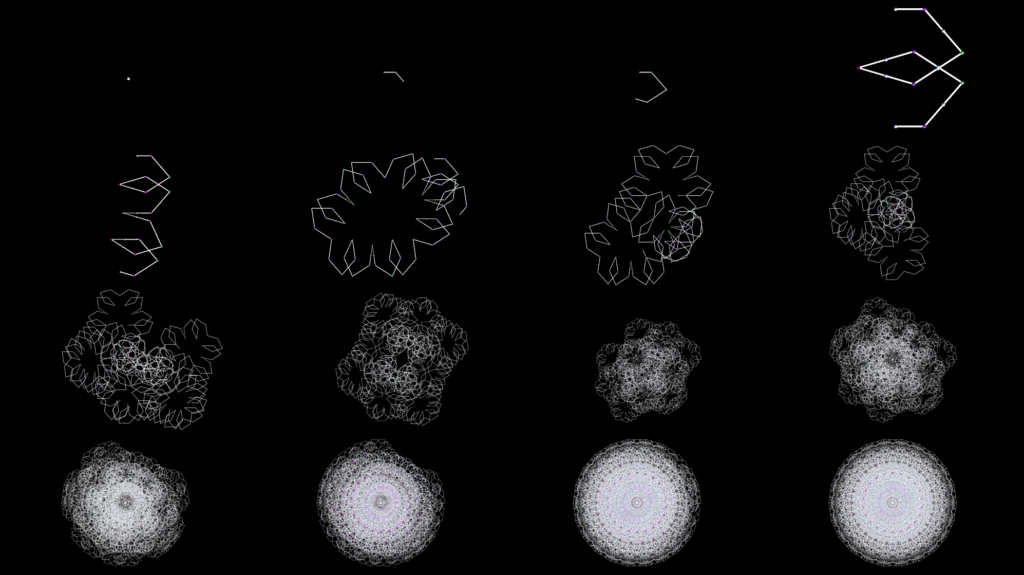
Base Angle: 56.25 degrees (5pi/16 radians)
Shape Type: Fractal (1-iteration cycle)

Base Angle: 60 degrees (pi/3 radians)
Shape Type: Fill-In (complete from 7 iterations on)
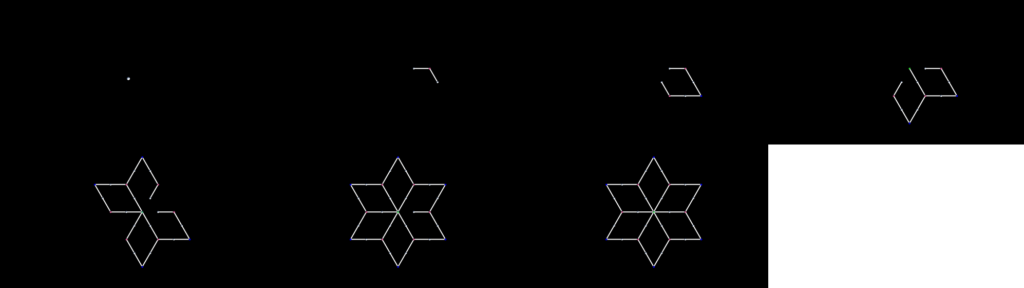
Base Angle: 67.5 degrees (3pi/8 radians)
Shape Type: Fractal (1-iteration cycle)
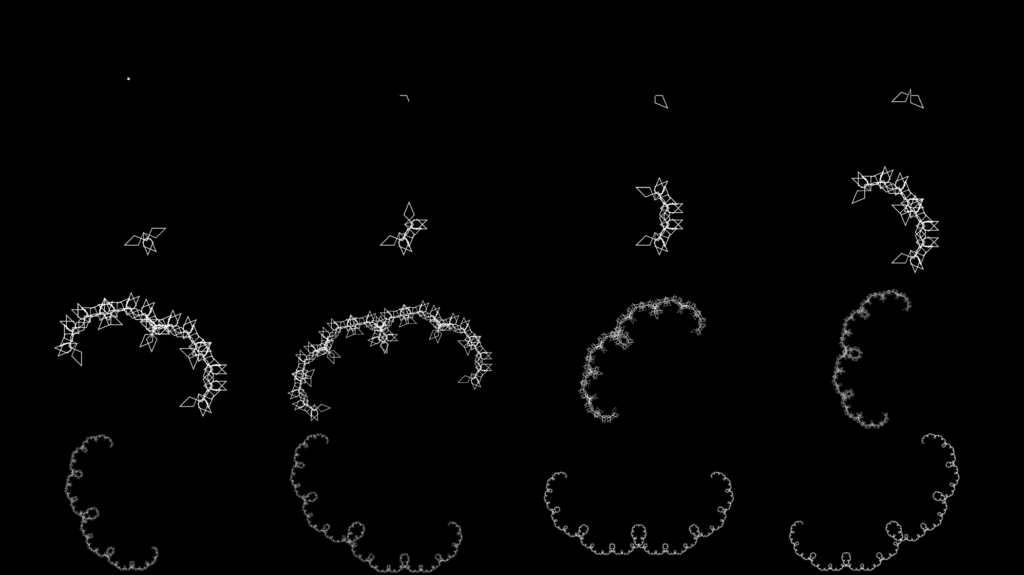
Base Angle: 77.14 degrees (3pi/7 radians)
Shape Type: Fill-In (complete after 9 iterations)
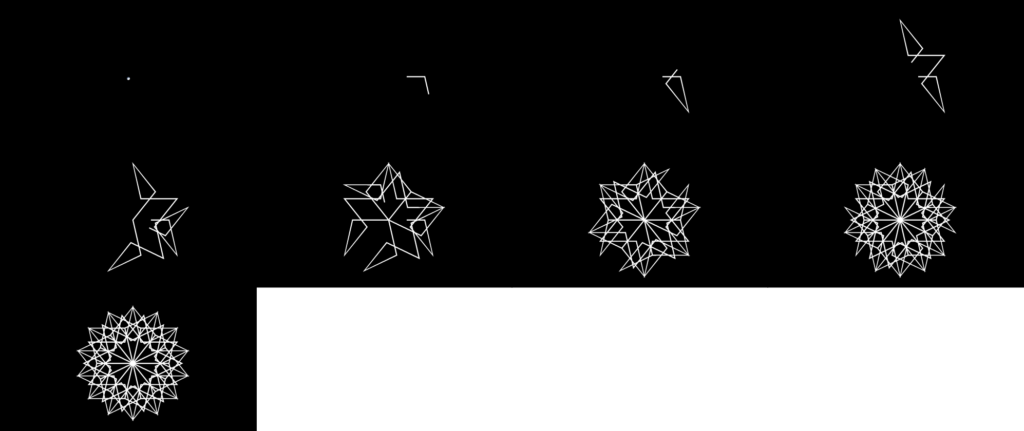
Base Angle: 78.75 degrees (7pi/16 radians)
Shape Type: Fractal (1-iteration cycle)
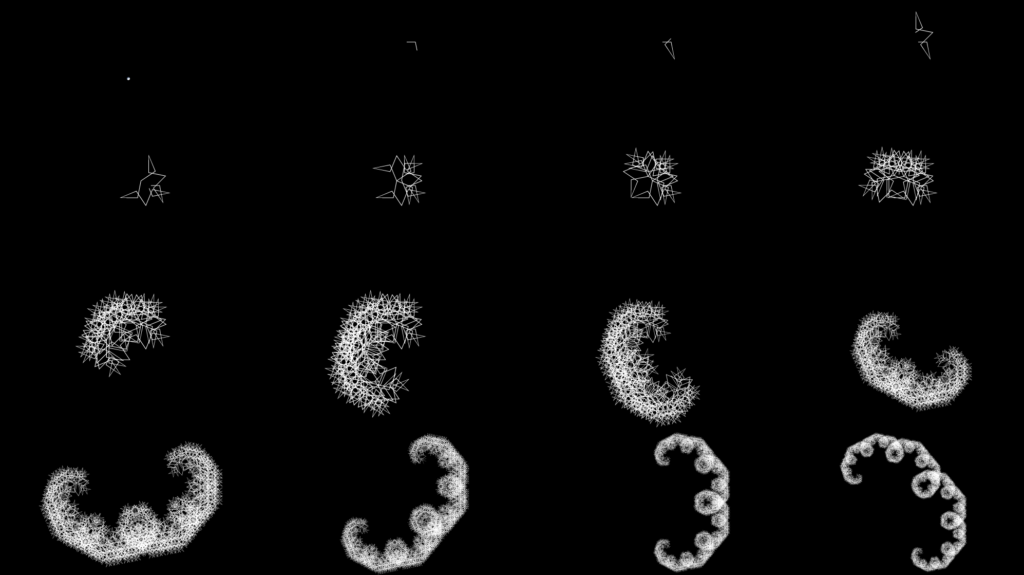
Base Angle: 90 degrees (pi/2 radians)
Shape Type: Fractal (Lévy C Curve/Lévy Dragon) (1-iteration cycle)

Base Angle: 102.86 degrees (4pi/7 radians)
Shape Type: Fractal (3-iteration cycle)

Base Angle: 108 degrees (3pi/5 radians)
Shape Type: Fill-In (complete from 9 iterations on)
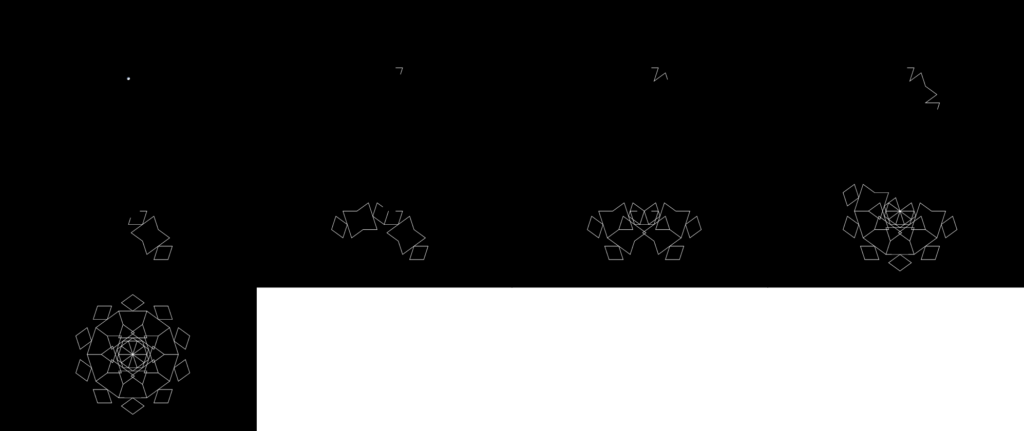
Base Angle: 114.55 degrees (7pi/11 radians)
Shape Type: Fill-In (complete from 9 iterations on)
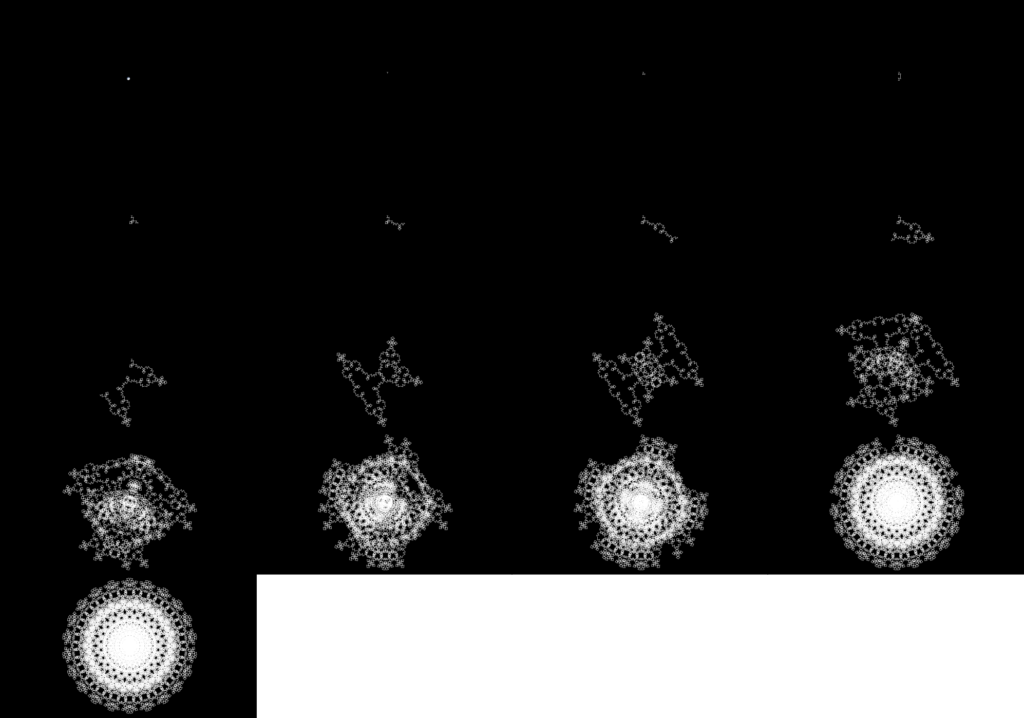
Base Angle: 120 degrees (2pi/3 radians)
Shape Type: Fractal (Lévy Diamond) (2-iteration cycle)

Base Angle: 125.22 degrees (16pi/23 radians)
Shape Type: Fractal (11-iteration cycle)

Base Angle: 144 degrees (4pi/5 radians)
Shape Type: Fractal (4-iteration cycle)

Base Angle: 150 degrees (5pi/6 radians)
Shape Type: Fractal (2-iteration cycle)

Base Angle: 161.05 degrees (17pi/19 radians)
Shape Type: Fuzzy?